Variables for analysis of hinge geometry

from sympy import *
import math
import numpy as np
import matplotlib.pyplot as plt

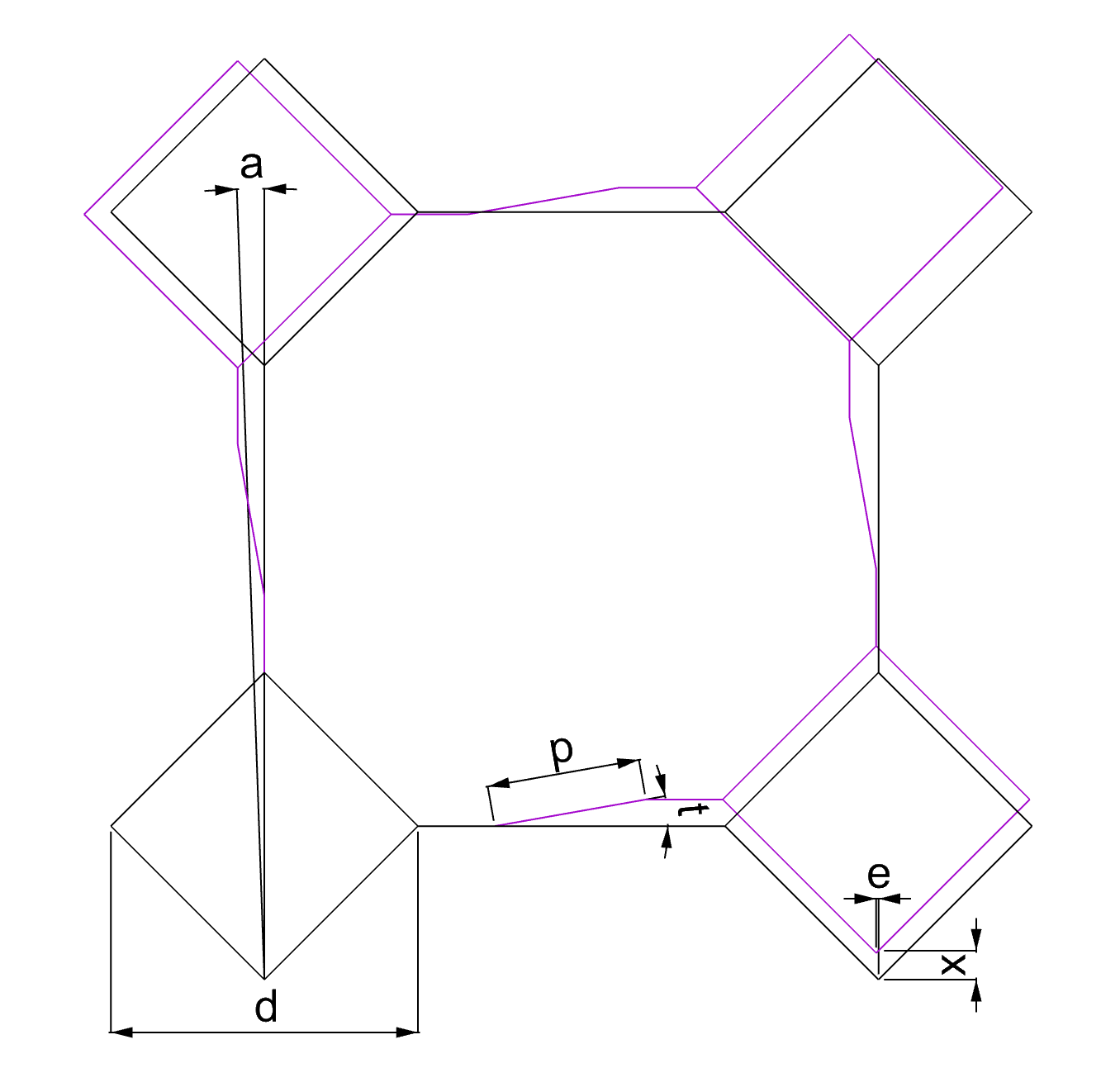
def calc_geometry(pitch,displacement,hinge):
    d = pitch
    x = displacement
    p = hinge*d
    t = asin(x/p)
    e = p*(1-cos(t))
    return d,p,x,t,e

d,p,x,t,e = calc_geometry(70.0,5.0,0.5)

print("pitch = " + str(d) + "mm   " + "hinge = " + str(p) + "mm   " + "displacement = " + str(x) + "mm   ")
print("error = " + str(round(e,2)) + "mm   " + "hinge angle = " + str(round(math.degrees(t),1)) + " deg")

pitch = 70.0mm   hinge = 35.0mm   displacement = 5.0mm   
error = 0.36mm   hinge angle = 8.2 deg

def plot_error_based_on_displacement(hinge):
    x = 2.0
    X = []
    E = []
    T = []
    for i in range(10):
        d,p,x,t,e = calc_geometry(70.0,x,hinge)
        x = x + (i*0.5)
        X.append(x/d)
        E.append(e)
        T.append(math.degrees(t))
    #print(E)
    #print(T)
    fig = plt.figure(figsize=(20,12), facecolor="white")
    t1 = "Horizontal displacement and hinge angle for p = " + str(hinge)
    plt.suptitle(t1, fontsize=14)
    ax1 = plt.subplot(221)
    ax2 = plt.subplot(222)
    ax1.scatter(X,E,color="#004da0")
    ax1.set_xlabel('Displacement as % of lattice pitch (x/d)')
    ax1.set_ylabel('Horizontal displacement required of linear actuator (e mm)')
    ax2.scatter(X,T,color="#004da0")
    ax2.set_xlabel('Displacement as % of lattice pitch (x/d)')
    ax2.set_ylabel('Hinge angle (t deg)')
    plt.show()

plot_error_based_on_displacement(0.4)
plot_error_based_on_displacement(0.6)
plot_error_based_on_displacement(0.7)

Affect of hinge length on hinge bend

Configuration with differing hinge lengths for constant bend angle

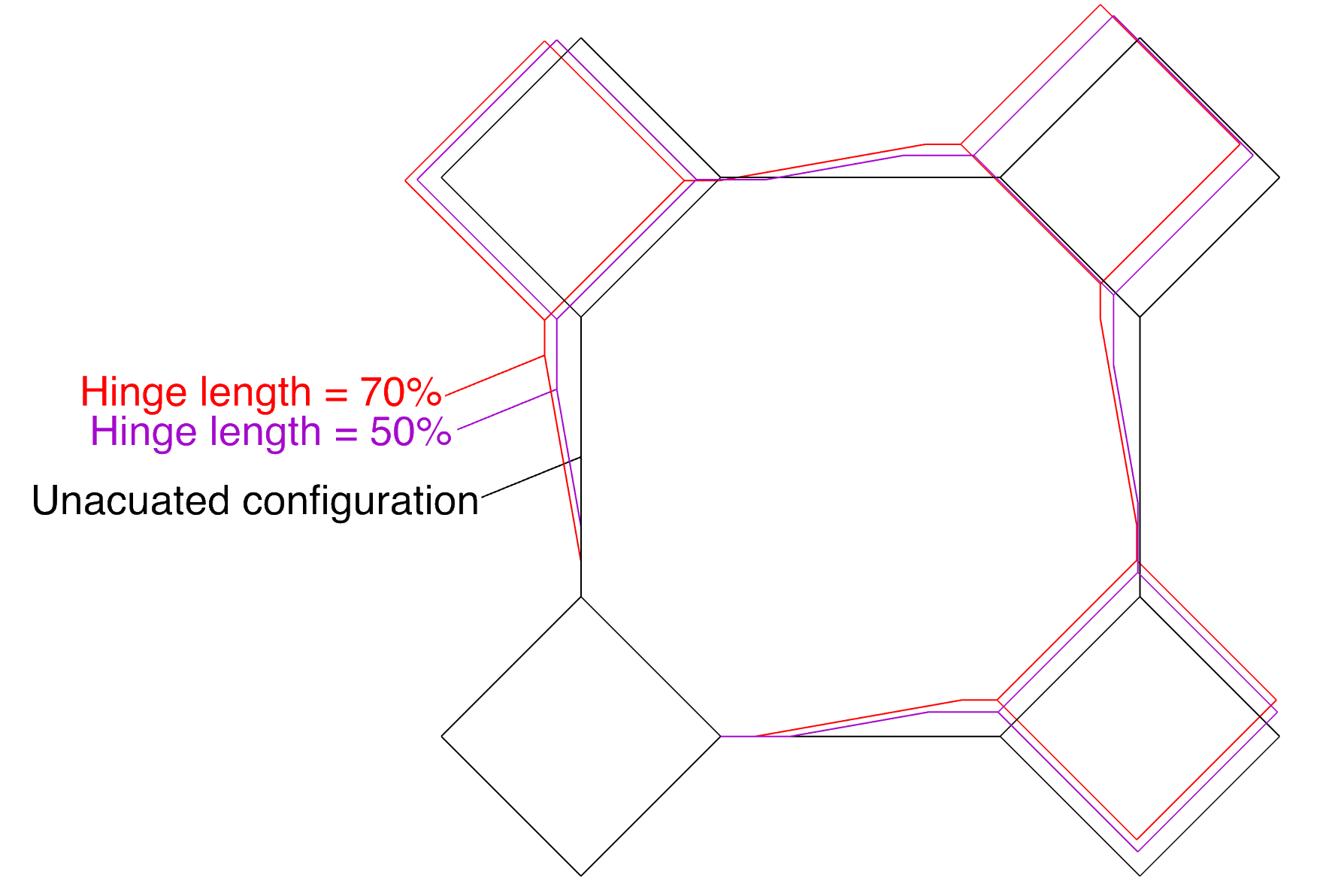
Configuration with differing hinge lengths for constant vertical displacement

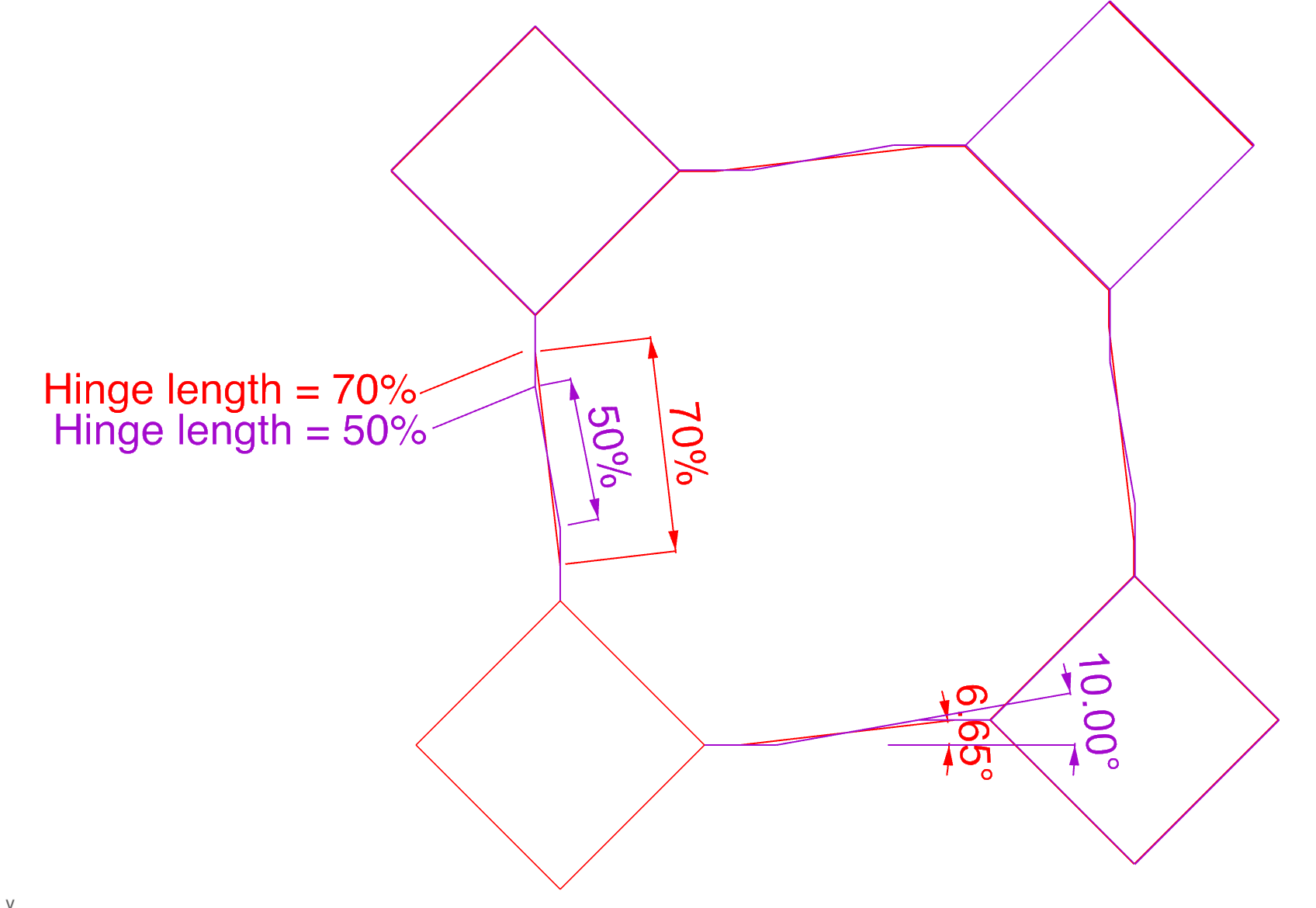
When the central section of the hinge is larger in proportion to the overall length, a shallower bend angle is required to produce the same displacement.

Affect of hinge bend on off-axis displacement

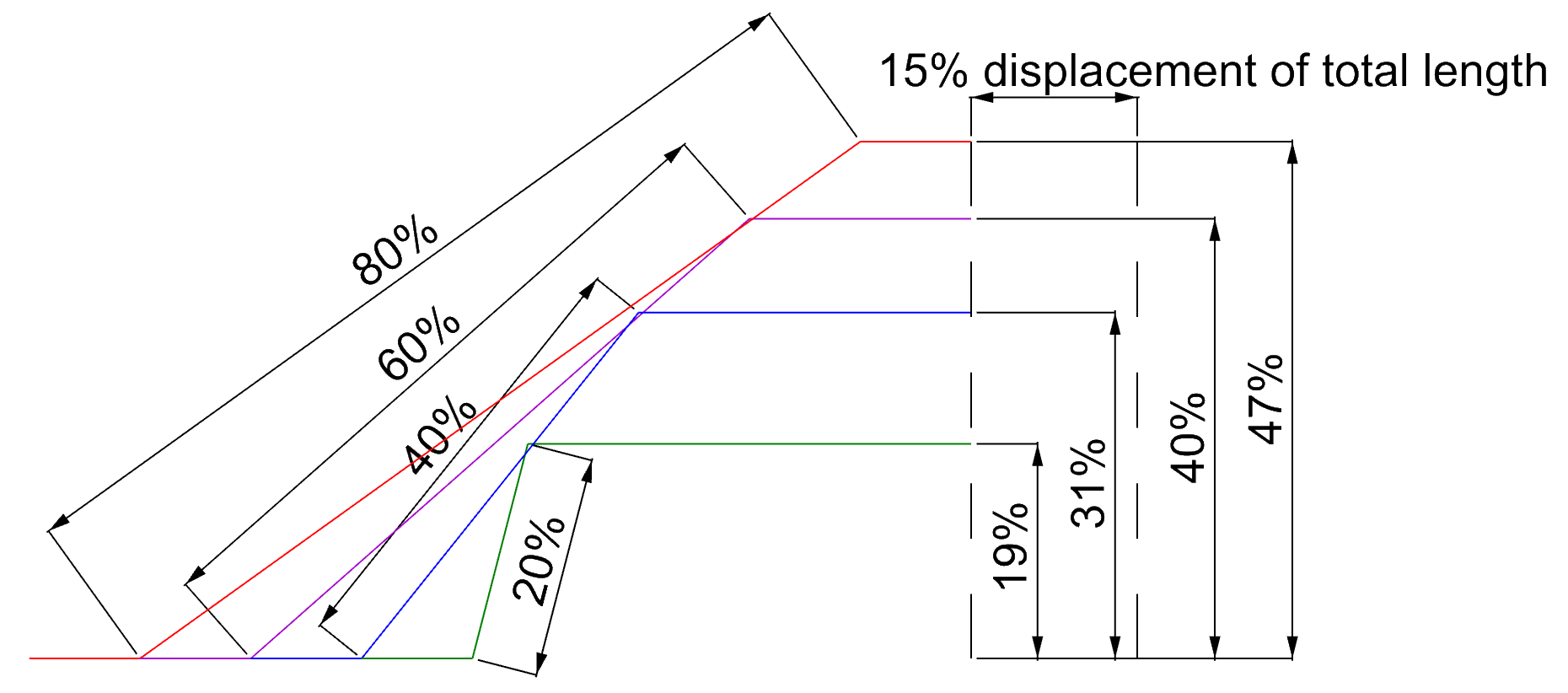
The larger the hinge length as a proportion of the total length, the larger the off-axis displacement. E.g 15% retraction of a hinge with 80% hinge length requires in 47% off axis displacement.